Christoforos Moutafis (University of Manchester)
Magnetic skyrmions are quasi-particle nanoscale magnetic spin configurations with a whirling vortex-like spin structure (Fig. 1a) with distinct topological properties [1,2] and intriguing dynamics [3,4]. The recent demonstrations from various groups of room temperature chiral skyrmions and their dynamical response are a first step for controlling their behaviour. Their ultra-small size, ability to move with low electrical current densities and robustness makes them excellent candidates for integration in next generation spintronics devices. In practice, chiral skyrmions can arise due to the interplay between the anisotropy and long-range dipolar energy with the short-range symmetric Heisenberg and antisymmetric Dzyaloshinskii-Moriya (DMi) exchange interactions [1,2].
They can span from tens of nanometers in diameter, behaving as classical quasi-particles exhibiting large inertia [4], down to the ~1 nanometer size. They are endowed with topological protection that can, practically, make them robust with enhanced tolerance to material defects present in devices. Recently, chiral skyrmions (sub-100nm) have been observed at room temperature in technologically relevant multilayers, confined in nanostructures, e.g. [5,6]. In fact, nanomagnets, can host a plethora of skyrmionics spin configurations that can also behave as quasi-particles (e.g. Fig. 2b)). Any possible integration in skyrmionic devices will necessarily involve controlled nucleation/generation and propagation of skyrmions, which is an active research topic e.g. [7,8]. A next step towards the development of skyrmionic devices is to shed light on the mechanisms of creation/destruction of topological charge in defects, which are present in realistic systems [9]. Such objects, like the prominent magnetic skyrmions, are promising candidates for future next generation skyrmion-based devices with diverse functionality such as memory [2], Boolean computing [10], stochastic computing [11], reservoir computing [12], biomimetic and artificial neuronal behavior [13-15].
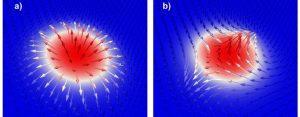
Figure 1 A (a) Néel type skyrmion and (b) an antiskyrmion spin configuration.
References
[1] N. Nagaosa and Y. Tokura, Nat. Nanotech. 8, 899 (2013).
[2] A. Fert, V. Cros, and J. Sampaio, Nature Nanotechnology 8, 152 (2013).
[3] C. Moutafis, S. Komineas, J.A.C. Bland, Physical Review B 79, 224429 (2009).
[4] F. Büttner, C. Moutafis, et al., Nature Physics 11, 225 (2015).
[5] C. Moreau-Luchaire, C. Moutafis, et al., Nature Nanotechnology 11, 444 (2016).
[6] O. Boulle, J. Vogel, et al., Nature Nanotechnology 11, 449 (2016).
[7] S. Woo, K. Litzius, et al., Nature Materials, 15, 501 (2016).
[8] W. Legrand,…, C. Moutafis, et al., Nano Letters, 17 (4), 2703 (2017).
[9] L. Pierobon, C. Moutafis, Y. Li, J. F. Löffler, M. Charilaou, Scientific Reports, 8, 16675 (2018).
[10] M. Chauwin, …, C. Moutafis, J. S. Friedman https://arxiv.org/abs/1806.10337 (2018).
[11] D. Pinna, F.A. Araujo, et al., Phys. Rev. Appl. 9, 064018 (2018).
[12] D. Prychynenko, M. Sitte, et al., Phys. Rev. Appl. 9, 014034 (2018).
[13] S. Li, W. Kang, et al., Nanotechnology 28, 31LT01 (2017).
[14] Y. Huang, W. Kang, et al., Nanotechnology 28, 1 (2017).
[15] T. Bhattacharya, S. Li, Y. Huang, W. Kang, W. Zhao and M. Suri, IEEE Access, 7, 5034 (2019).
